Right now I am solving the 99-scala-problems. Again!!!
This time around I am using them to learn more about what it means to be an Augmented Software Engineer (ASE). Just subscribe to the podcast to follow along.
P50 is to build a Huffman tree and to return the set of Huffman codes for the given string.
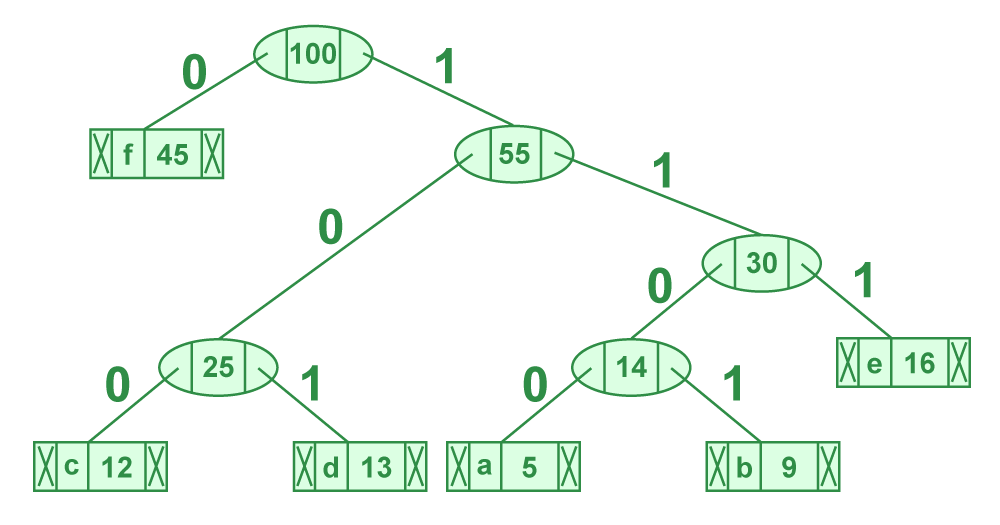
codeium found a good implementation, but struggled to find tests that worked.
I then tried various websites ([1], [2], [3], [4]) to test various strings and noticed that the trees and the resulting set of codes are different between the implementations. Even more interesting for the same implementation the set is different when you reverse the string.
That felt strange to me. My expectation was that the same set of (character, frequency) tuples will always create the same set of Huffman codes.
So I started digging. Here is what chatGPT had to say about it …
You're absolutely correct to ask this question. When there are multiple
nodes with the same weight in the priority queue, the behavior can indeed
depend on how the priority queue resolves ties. This can result in different
tree structures, which could lead to different Huffman codes, even though
all such codes would still represent valid Huffman encodings (i.e., they
would satisfy the prefix-free property and correspond to the correct
frequencies).
So it seems that Huffman codes can be different for the same set of
(character, frequency) pairs, because there is an edge case where you
need to dequeue the top two nodes from the priority queue with the
lowest weight. If there are three or more nodes that have the same
lowest weight it depends on the order the nodes where put into the
queue and the internal implementation of the queue, which two of the
three or more nodes are the top nodes that get dequeued.
To address this and to make the set of generated Huffman codes
deterministic I changed the implementation to keep track of the largest
character in the sub-tree and sort the queue by weight(descending) and maxChar(ascending) and use the guaranteed-to-be-unique maxChar as a
tie-breaker for the sorting of the priority queue. This will ensure
that we always dequeue the same two nodes, regardless of the order the
nodes were put into the queue and regardless of the internal
implementation of the queue.
Note: This would (obviously) also work with minChar as a
tie-breaker. Your call.
With that we get two very nice benefits: First, we can change the
signature of huffman() from huffman(List of (character, frequency) pairs): returning List of (character, huffman-code) pairs to
huffman(Set of (character, frequency) pairs): returning Set of (character, huffman-code) pairs, which feels much more natural and
correct, because the huffman codes you get should not depend on the
order of the (character, frequency) pairs.
And second, we can now change the implementation of the priority queue without (potentially) breaking our tests (because without the tie-breaker the implementation of the priority queue decides which two nodes are top of the queue).
That also means that we will always get the same set of Huffman codes
for the same set of frequencies (means huffman(text) == huffman(text.reverse), which is not true for most of the
implementations out there.
That was an interesting one.
And it drives home one of the main/major points that you need to consider as an Augmented Software Engineer: The code you get is a suggestion. A starting point. You are well-advised to reason about it and dig into it, if/when you do not understand something.
I was very close to moving on to the next problem, because getting the first/initial implementation and the first/initial tests work was a very fast and smooth experience (with the help of codeium).
It was only when I started to question the implementation and the test against my own understanding, that I realized that something is not quite right.
With that additional step/work we are now in a good place: We saved some time to get the initial implementation done, but I also have a much deeper understanding how Huffman trees work and how to implement them so that they are more deterministic.
Feel free to check out the code.